Baustein 6.7

Proportionen

../res/aoo-tabellendokument.png
  • Zuordnungstabelle für eine proportionale Zuordnung anlegen
  • Zuordnungstabelle mit Formeln proportional ergänzen
  • Rechentabelle kopieren und einsetzen
  • XY-Diagramme für Zuordnungstabellen erstellen
../res/unten.png Hallo!
../res/unten.png Tabellendokument erzeugen und speichern
../res/unten.png Tabelle für eine proportionale Zuordnung vorbereiten ../res/aoo-odt.png
../res/unten.png Tabelle für eine Zuordnung mit überlegten Rechenwegen proportional ergänzen ../res/aoo-odt.png
../res/unten.png Tabelle für eine Zuordnung mit dem „Schluss über die 1“ proportional ergänzen ../res/aoo-odt.png
../res/unten.png Ausgangswerte variieren ../res/aoo-odt.png
../res/unten.png Kalkulation optisch prüfen (Zusatzoption)
../res/unten.png Graph der Zuordnung als XY-Diagramm herstellen
../res/unten.png Arbeit abschließen ../res/aoo-ods.png


Voraussetzung für die Bearbeitung dieses Bausteins


../res/oben.png Hallo!

res/adele.jpg

Quelle: http://magic983.com/event/adele-madison-square-garden-2/
Die nebenstehende Abbildung ist eine Verkleinerung eines Portraits des Popstars Adele.

Verkleinerung? „Es handelt sich wohl eher um eine Verzerrung als um eine Verkleinerung!“ wirst du dir sagen, „da hat jemand wahrscheinlich etwas falsch gemacht ...“

Das Portrait von Adele besteht im Original aus 1278 Pixeln in der Breite und 852 Pixeln in der Höhe. Wenn du auf das Bild klickst, wird es dir in einem separaten Fenster (oder Tab) in Originalgröße angezeigt.


Pixel

Bei dem Begriff Pixel handelt es sich um ein englisches Kunstwort, das aus „picture“ und „element“ zusammengesetzt wurde. Das deutsche Gegenstück ist das Wort „Bildpunkt“.

Das Portrait von Adele besteht also im Original aus insgesamt 1278 × 852 = 1.088.856 Bildpunkten.

Hier gibt es noch mehr Informationen zum Thema „Pixel“: → Wikipedia-Artikel zum Begriff „Pixel“


Die verzerrte Abbildung des Portraits ist deutlich kleiner als das Original. Das liegt daran, dass diese Webseite das Bild in einen Bilderrahmen quetscht, der nur 568px breit und 142px hoch ist.

Wie du leicht nachrechnen kannst, ist der Bilderrahmen in der Breite und in der Höhe jeweils um 710 Pixel kleiner als das Original, das er anzeigt:
Aber wieso, wirst du dich fragen, kommt es dann zu dieser merkwürdigen Verzerrung? Breite und Höhe wurden doch um denselben Wert verringert! Adele müsste zwar kleiner, aber trotzdem wohl proportioniert erscheinen ...

Halt! Dadurch, dass wir denselben Wert von 710 px von der Breite und der Höhe subtrahieren, haben wir die Proportion des Bildes verändert. Statt Proportion können wir auch Seitenverhältnis sagen:



 Breite
 Höhe
Original
 1278px
 852px
Seitenverhältnis
 3
 2
Rechnung
  BreiteHöhe=1278852=3·4262·426=32\frac{Breite}{Höhe} = \frac{1278}{852} = \frac{3 · 426}{2 · 426} = \frac{3}{2} = 3:2 (=1,5)
Kommentar
 Der größte gemeinsame Faktor der Abmessungen des Originals ist 426.

Wenn wir diesen Faktor weglassen, wird aus dem Verhältnis 1278 : 852 das Verhältnis 3:2.

Folgerung: Im Original ist die Breite 1,5 mal so groß wie die Höhe.


Breite
 Höhe
Bilderrahmen in der Webseite
 568px
 142px
Seitenverhältnis
 4
 1
Begründung  BreiteHöhe=568142=4·1421·142=41\frac{Breite}{Höhe} = \frac{568}{142} = \frac{4 · 142}{1 · 142} = \frac{4}{1} = 4:1 (= 4)
Kommentar
 Der größte gemeinsame Faktor der Abmessungen ist 142.

Wenn wir diesen Faktor weglassen, wird aus dem Verhältnis 568 : 142 das Verhältnis 4:1

Folgerung: Im Bilderrahmen ist die Breite 4 mal so groß wie die Höhe.

Zur Erinnerung: Erweitern und Kürzen von Brüchen


Ebenfalls zur Erinnerung: Aus Summen kürzen nur die Dummen

Wie falsch es ist, von Zähler und Nenner denselben Betrag zu subtrahieren, zeigt das folgende Beispiel:
  • Breite des Bilderrahmens: 1278px – 851px = 427px
  • Höhe des Bilderrahmens: 852px – 851px = 1px
Jetzt würde das Bild zu einem 427 Pixel langen Strich entarten, der nur 1 Pixel hoch ist. Das kann keine proportionale Wiedergabe des Originals sein!

Proportionale Zuordnung

In der Mathematik sprechen wir von einer proportionalen Zuordnung, wenn die einander zugeordneten Werte immer im gleichen Verhältnis stehen.

Die Zuordnung

„Gewählte Höhe des Bildes → Zugehörige Breite des Bildes“

ist also genau dann proportional, wenn das Verhältnis  BreiteHöhe\frac{Breite}{Höhe}  bei allen Wertepaaren gleich groß ist.

Konsequenzen:


Nachdem wir uns noch einmal das mathematische Prinzip der Proportionalität klar gemacht haben, werden wir nun in zwei Beispielen zeigen, wie Adeles Bild in einem Bilderrahmen, der kleiner als das Original ist, proportioniert dargestellt werden kann.

1. Beispiel: Anpassung der Breite mittels Bruchrechnung

res/adele.jpg
  BreiteHöhe=1278852=6·2136·142=213142\frac{Breite}{Höhe} = \frac{1278}{852} = \frac{6 · 213}{6 · 142} = \frac{213}{142}

Das bedeutet: Wenn der Bilderrahmen nur 142 Pixel hoch sein soll, dann darf der Bilderrahmen auch nur 213 Pixel breit sein, wenn die Proportion erhalten bleiben soll.

Falls du es nicht glauben solltest, der Bilderrahmen hat jetzt so wie das Original das Seitenverhältnis 3:2.

  BreiteHöhe=213142=71·371·2=32\frac{Breite}{Höhe} = \frac{1278}{852} = \frac{6 · 213}{6 · 142} = \frac{213}{142}

Dem Bilderrahmen auf der rechten Seite haben wir die Breite 213px und die Höhe 142px gegeben; offensichtlich wird jetzt Adele im korrekten Seitenverhältnis dargestellt.

2. Beispiel: Anpassung der Höhe unter Verwendung eines Taschenrechners

res/adele.jpg
Hier geht also die Rechnung nicht so schön auf, wie im 1. Beispiel.

Weil wir die Breite und Höhe von Bilderrahmen auf Webseiten aber immer nur ganzzahlig angeben dürfen, bleibt uns nichts anderes übrig, als das Ergebnis zu runden.

In den folgenden Abschnitten möchten wir dir zeigen, wie du mit einem OpenOffice Tabellendokument die Abmessungen eines Bildes auf beliebige Weise proportional abändern kannst, ohne dich mit der Bruchrechnung herumzuschlagen.

Durch die Erstellung dieser Kalkulation wirst du lernen, wie du immer eine proportionale Zuordnung mit einem Tabellen­dokument entwickeln kannst. Der Mathematik­unterricht der Stufe 7 wird dir im Übrigen zeigen, dass unsere Welt von lauter proportionalen Zuordnungen nur so wimmelt! Du lernst also mit diesem ITG-Baustein richtig viel „Weltmathematik“.

Auf geht's!


Ergänzung: Bildschirmauflösung ppi

Wie scharf ein Bild auf einem Bildschirm erscheint, hängt davon ab, wie hoch die „Auflösung“ des Bildschirms ist, das heißt, wie viele Pixel der Bildschirm auf einem Zoll (= 2,54 cm) unterbringt.

Je mehr Pixel ein Bildschirm auf einem Zoll unterbringt, desto schärfer ist sein Bild.

Ein typischer Wert für Computer-Monitore ist „90 Pixel pro Zoll“, auf englisch „90 pixelper inch“, kurz 90 ppi. Bessere Monitore kommen auf Werte um 110 ppi, das aktuelle Retina-Display der Firma Apple sogar auf 227 ppi.

Auf einem Bildschirm mit einer Auflösung von 90 ppi ist das Originalbild von Adele ...

Auf einem Bildschirm mit einer Auflösung von 227 ppi ist das Originalbild von Adele ...

Merke: Bei Verwendung der gleichen Anzahl von Originalpixeln ist ein schärfer dargestelltes Bild kleiner als ein weniger scharf dargestelltes.




../res/oben.png Tabellendokument erzeugen und speichern

../res/aoo-tabellendokument.png OpenOffice erzeugt ein leeres Tabellendokument und zeigt es dir in einem Fenster an. Die Titelleiste weist den Namen „Unbenannt1“ aus; damit wird dir verdeutlicht, dass dieses Dokument nicht gesichert ist.

../res/oben.png Tabelle für eine proportionale Zuordnung vorbereiten

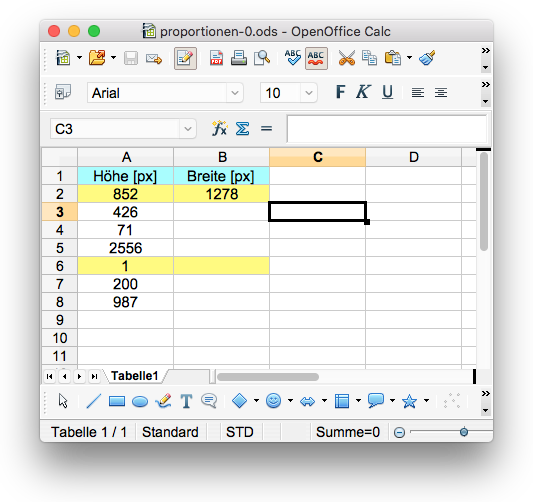
res/02-proportionen-0.png
Es hat sich in der Mathematik eingebürgert, Zuordnungen zwischen zwei Größen als gerichtet anzusehen, das heißt:
In der rechts abgebildeten Tabelle wird die 1. Größe (Höhe des Bildes) in der Spalte A und die 2. Größe (Breite des Bildes) in der Spalte B wiedergegeben.

Die eingetragenen Höhen haben wir willkürlich gewählt und fragen uns nun, ob OpenOffice uns helfen kann, die passenden Breiten so zu bestimmen, dass es sich insgesamt um eine proportionale Zuordnung handelt.
Sichere die vorgenommene Anlage der Tabelle:
../res/aoo-odt.png
proportionen-0.ods
Falls du es möchtest, kannst du dir durch einen Klick auf das Symbol auf der rechten Seite das bisher erreichte Zwischenergebnis auf deinen Rechner laden.




../res/oben.png Tabelle für eine Zuordnung mit überlegten Rechenwegen proportional ergänzen

Im ersten Abschnitt dieses Bausteins haben wir gelernt, dass wir nur dann eine proportionale Zuordnung erhalten, wenn wir bei der Zielgröße (Breite) mit denselben Faktoren multiplizieren oder durch dieselben Faktoren dividieren, die wir bei der Ausgangsgröße (Höhe) anwenden.

Die folgende Grafik zeigt, welche Rechenwege angewandt werden können, um aus der Originalhöhe von 852 px die Höhen 426 px, 71 px, 2556 px und schließlich 1 px zu gewinnen.

Ausgehend von der Höhe 1 px lässt sich dann, wie die untersten beiden Zeilen der Tabelle zeigen, jede andere Höhe durch eine einfache Multiplikation gewinnen.

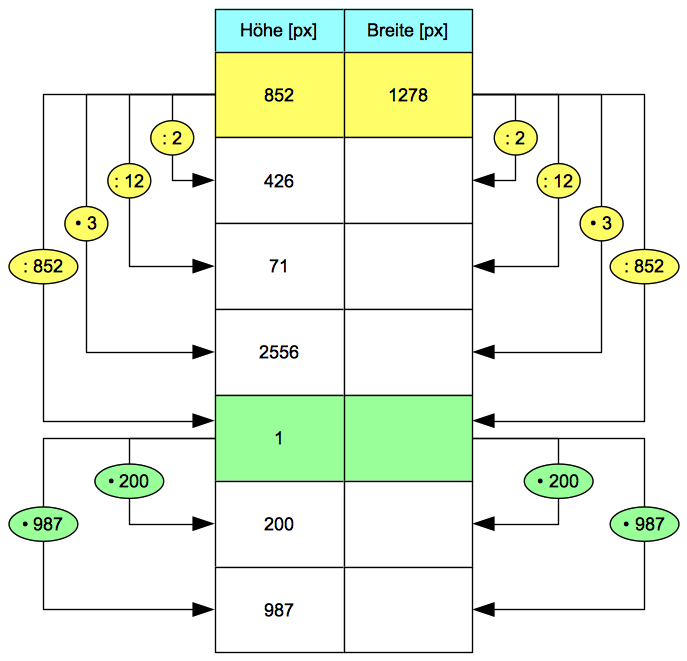
res/03-rechenwege1.png



res/04-proportionen-1.png
Dieselben Rechenwege kannst du nun als Formeln in das Tabellendokument eingeben:
Wenn du es richtig machst, erhältst du die rechts abgebildete Darstellung des Tabellendokuments.


Falls du es möchtest, kannst du das neue Zwischenergebnis auf deinen Rechner laden.

../res/aoo-odt.png
proportionen-1.ods







../res/oben.png Tabelle für eine Zuordnung direkt mit dem Schluss über die 1 proportional ergänzen

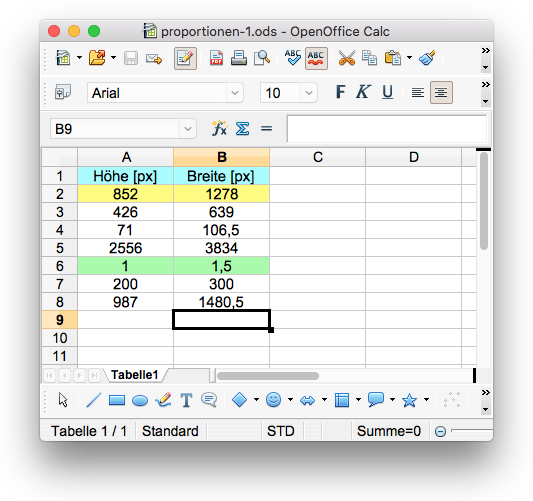
Falls du schön aufgepasst und mitgedacht hast, ist dir sicherlich Folgendes aufgefallen:
Ist es dann nicht viel geschickter, wenn wir sofort den Weg über die Höhe 1px einschlagen? Wir können zu jeder neuen Höhe h die zugehörige Breite ohne weitere Erkundungen von Rechenwegen ermitteln, indem wir die Originalbreite 1278 durch 852 teilen und das Zwischenergebnis (Das ist ja die Breite, die zur Höhe 1px gehört!) mit der neuen Höhe h multiplizieren:


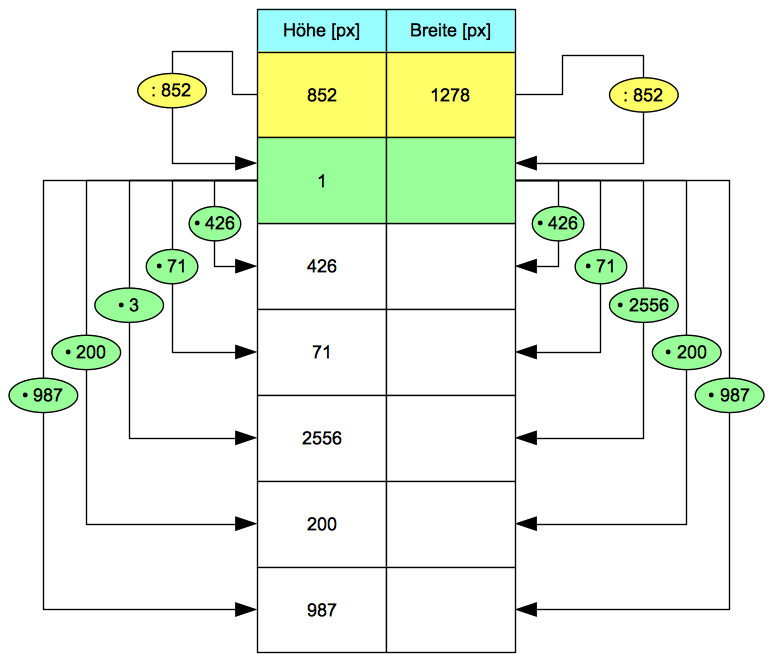
res/05-rechenwege2.png

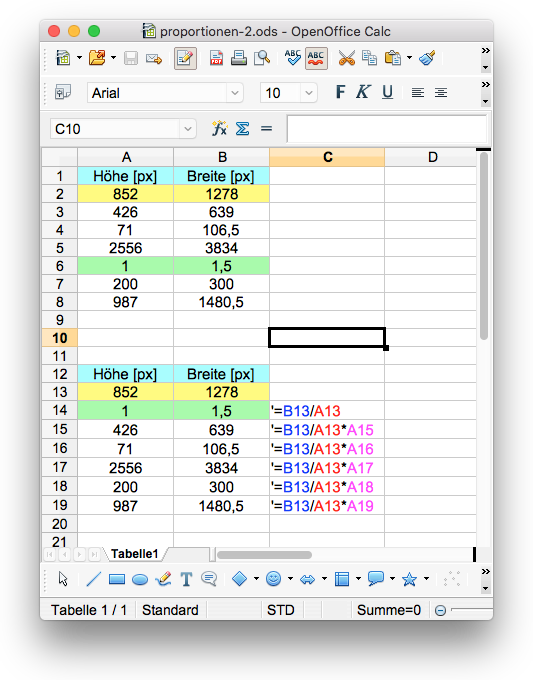
res/06-proportionen-2.png

Wir legen daher die Kalkulation noch ein zweites Mal etwas tiefer ab Zeile 12 in dem Tabellendokument an.

In der Abbildung rechts zeigen wir in der Spalte C die Formeln, die wir in der Spalte B benutzen.

Zuerst kopieren wir den Kopf der Kalkulation:
Dann setzen wir darunter den „Schluss auf die 1“:
Nun verbessern wir die Formel in der Zelle B14, die durch den Kopiervorgang ungültig geworden ist:
Nach diesen Vorbereitung ergänzen wir die eigentliche proportionale Schlussrechnung.
Wie du siehst, kannst du mit einer Tabellenkalkulation proportionale Werte auf sehr elegante Weise ohne Bruchrechnung ermitteln. Der Schlüssel dazu ist der „Schluss über die 1“, den du mit Hilfe der Tabellenzeile 14 sichtbar machst.

Es sollte dir nachträglich klar werden, dass diese Tabellenzeile 14 in Wirklichkeit überflüssig ist! Du könntest diese Zeile glatt weglassen, denn die Formeln im Zellbereich B15:B19 benutzen die Zeile 14 nicht.

../res/aoo-odt.png
proportionen-2.ods
Falls du es möchtest, kannst du dir durch einen Klick auf das Symbol auf der rechten Seite das bisher erreichte Zwischenergebnis auf deinen Rechner laden.




../res/oben.png Ausgangswerte variieren

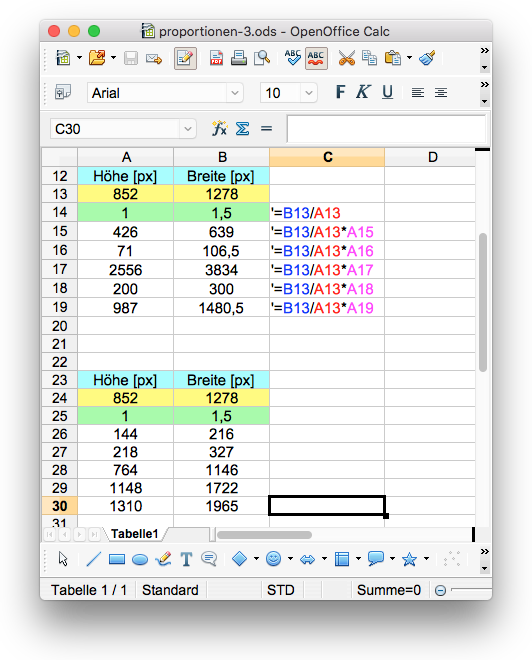
res/07-proportionen-3.png
Der besondere Vorzug einer Tabellenkalkulation besteht, wie du bereits mehrfach erlebt hast, in der Möglichkeit, zu abgeänderten Eingaben sofort die korrigierten Ergebnisse zu erhalten.

Damit du die Entwicklung des Gedankenganges dieses ITG-Bausteins nicht aus den Augen verlierst, fertigen wir jedoch zunächst eine Kopie des Kalkulationsabschnitts an, bevor du die Daten veränderst.
Du verfügst nun über eine Kopie der Daten im Zellbereich A23:B30.
Du solltest dann sofort in der zweiten Spalte im Bereich B23:B30 die passenden Breiten geliefert bekommen. Diese Aktion zeigt dir, dass du mit Hilfe einer Tabellenkalkulation zu jedem Wert der Ausgangsgröße sofort den zugehörigen Wert der Zielgröße geliefert bekommst, sobald du die proportionale Zuordnung in der gezeigten Weise angelegt hast.

Wir gehen auf diesen Aspekt im übernächsten Abschnitt noch einmal ein.

../res/aoo-odt.png
proportionen-3.ods
Falls du es möchtest, kannst du dir durch einen Klick auf das Symbol auf der rechten Seite dieses Zwischenergebnis auf deinen Rechner laden.




../res/oben.png Kalkulation optisch prüfen (Zusatzoption)

Diesen Abschnitt kannst du ohne Kenntnisverlust überspringen.

Wir haben das Thema „Digitaler Bilderrahmen“ mit Bedacht gewählt, um dich in die Verwendung einer Tabellenkalkulation bei der proportionalen Rechnung einzuführen. Dieses Themenbeispiel ermöglicht es dir, die Ergebnisse deiner Rechnungen optisch zu prüfen. Trotz der guten mathematischen Argumente bleibt ja die Frage, ob die ermittelten Wertepaare (Höhe; Breite) tatsächlich zu verzerrungsfreien Darstellungen von Adeles Portrait führen.

Als Abmessungen für das Bild haben wir in diesem Textdokument eine Höhe von 8,52 cm und eine Breite von 12,78 cm gewählt. Wir haben also die Pixelangaben einfach in Hundertstel Zentimeter überführt. Diese Behauptung kannst du sofort prüfen:
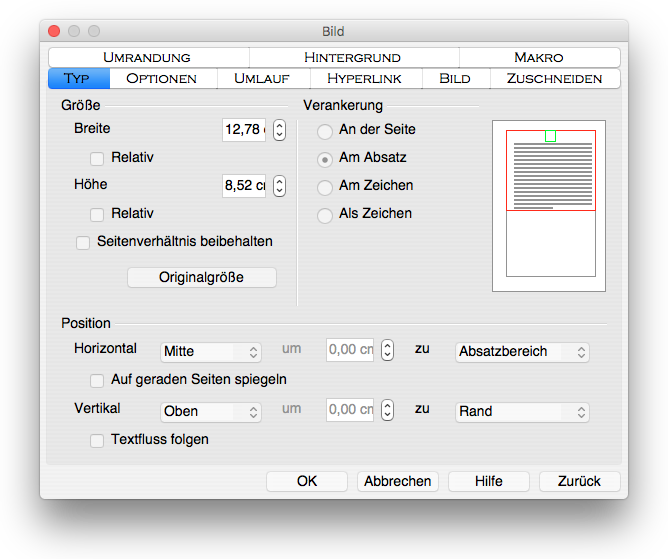
res/08-format.png
Für das Prüfverfahren ist es wichtig, dass die Option «Seitenverhältnis beibehalten» ausgeschaltet ist, denn andernfalls kannst du Höhe und Breite des Bildes nicht unabhängig voneinander eingeben:
Wir prüfen nun den ersten Wert, den wir in unserer Tabellenkalkulation errechnet haben:
Prüfe nun auf die gleiche Weise den zweiten Wert der Tabellenkalkulation:
Wenn du möchtest kannst du auf diese Weise fortfahren, um auch noch die Werte in den Tabellenzeilen 28, 29 und 30 zu überprüfen.

../res/oben.png Graph der Zuordnung als XY-Diagramm erstellen

In den vorangegangenen Bausteinen „Hitzefrei“ und „Schulwegzeiten“ hast du gelernt, eine Wertetabelle in einem Säulen-, Linien oder Balkendiagramm darzustellen. Jetzt sollst du die Wertetabelle der proportionalen Zuordnung

Höhe [px] → Breite [px]

in einem Diagramm darstellen. Dazu sollst du die Daten verwenden, die du zuletzt eingegeben und gesichert hast (siehe Abbildung im vorletzten Abschnitt).

Nachfolgend haben wir die Daten in den Zeilen 26 bis 30 (Das sind insgesamt fünf Wertepaare) einerseits in einem Liniendiagramm (linke Abbildung), andererseits in einem so genannten XY-Diagramm (rechte Abbildung) dargestellt. Welches ist wohl sinnvoller? Schau genau hin!

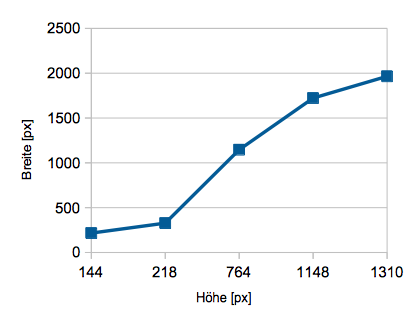
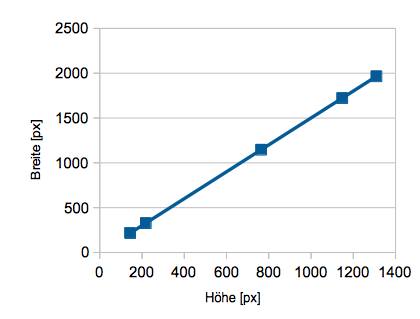
res/09-liniendiagramm.png      res/10-xy-diagramm.png

Wie du sicher schnell erkennst, werden in einem Liniendiagramm die Zahlenwerte der Höhen nicht beachtet; die Punkte sind horizontal paarweise gleich weit voneinander entfernt, obwohl der Unterschied zwischen 218 und 144 nur 74, zwischen 764 und 218 hingegen 546 beträgt. Ein Liniendiagramm ist strukturell mit einem Säulendiagramm verwandt, in dem die Säulen ja auch alle paarweise den gleichen Abstand voneinander haben.

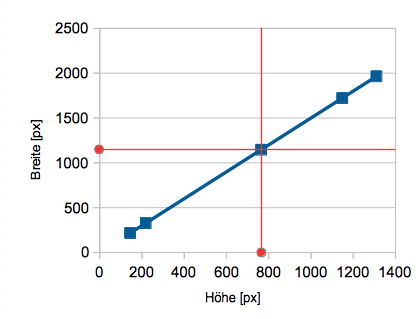res/11-ko-ystem.pngEin XY-Diagramm ist dagegen ein Graph in einem Koordinatensystem:
In der Abbildung auf der rechten Seite haben wir das Wertepaar

(Höhe; Breite) = (764; 1146)

 dargestellt.

Das XY-Diagramm zeigt in eindrucksvoller Weise, dass Graphen von proportionalen Zuordnungen stets Geraden sind, die durch den Ursprung verlaufen.
Fertig!


../res/oben.png Arbeit abschließen

../res/aoo-ods.png
proportionen-4.ods
Du hast nun den Baustein komplett bearbeitet und kannst daher deine Arbeit abschließen. Falls du Probleme hattest, es zu erreichen, kannst du dir hier auch mit dem Symbol auf der rechten Seite die fertige Lösung herunterladen.
Das fertige Dokument liegt zur Zeit auf dem Schreibtisch deines Rechners; dort sollte es nicht liegenbleiben.
Das war's für heute. Bis zum nächsten Mal!



Letzte Änderung: 22.10.2017